Equipollence (geometry)

In geometry, equipollence is a certain relationship between ordered pairs of points. A pair (a, b) of points and another pair (c, d) are equipollent precisely if the distance and direction from a to b are respectively the same as the distance and direction from c to d.

In affine spaces over a field

Let K be a field (which may be the field R of real numbers). An affine space E associated with a K-vector space V is a set provided with a mapping ƒ : E × E → V; (a, b) → ƒ(a, b) (the vector ƒ(a b) will be denoted 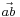\scriptstyle\vec{ab}) such that:

1) for all a in E and all 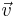\vec{v} in V there exist a single b in E such that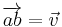 \overrightarrow{ab} = \vec{v}

2) for all a,b,c in E, 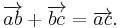\overrightarrow{ab} %2B \overrightarrow{bc} = \overrightarrow{ac} .

Definition:

Two bipoints (a, b) and (c, d) of ExE are equipollent if 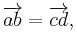\overrightarrow{ab} = \overrightarrow{cd} ,

when K=R (or K is a field of characteristic different from 2) then (a, b) and (c, d) are equipollent if and only if (a,d) and (b,c) have the same midpoint.

The concept of equipollence of bipoints can be also defined axiomatically.

External links